2-1-3 DCモータの回転速度と逆起電力
トルク定数KTのことをさらに洞察するために、モータが回転している状況を考えてみましょう。
これにはモータの発電作用が関係してきます。
発電作用と右手の法則
e = BLv ……(2.5)
e:発生電圧、逆起電力[V]B:磁束密度[T]
L:磁界中の電線長[m]v:速度[m/s]
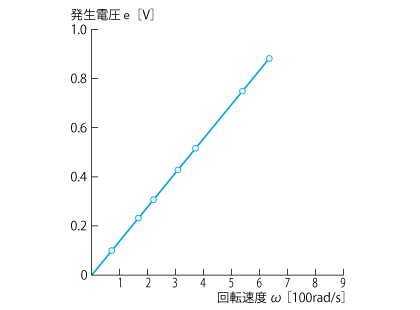
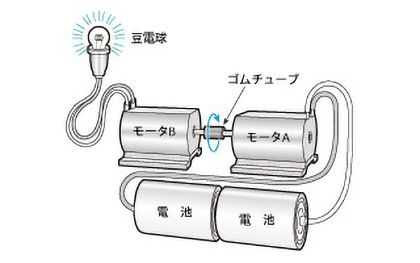
図2.6 のように2つのモータを連結し、一方のモータに豆電球を、他方のモータに電源を接続してモータを回すと、豆電球が点灯します。
この実験から、DCモータには発電作用があることがわかります。
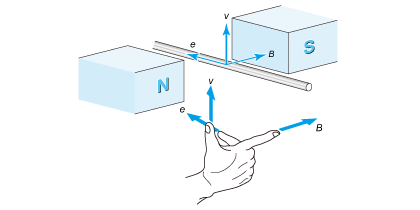
今度は図2.7 のように電流を流さずに、磁界を横切るように電線を速度vで動かすと、電線に電圧eが発生します。これを、先の図2.2 と比べてみましょう。
この電圧の向きは、フレミングの右手の法則によって決まります。この向きは図2.2 の電流の向きとは逆向きであり、電流を減らそうという作用になるために逆起電力と呼びます。電線がモータの巻線の一部であるとして、図2.3 を参照すると、電線の速度vはv=ωRと表せることがわかります。よってこの電線に現れる逆起電力は次式になります。
e=BLRω ……(2.6)
ω:回転速度[rad/s] R:回転半径[m]
つまり、逆起電力は回転速度ωに比例します。
実際のDCモータの場合には、すべてのコイルに作用する逆起電力が合算されて端子間に現れます。
これはやはり回転速度に比例するので逆起電力定数KEというものを使って表します。
e = KEω ……(2.7)
e:ここではモータ端子に現れる発生電圧(逆起電力)[V]
KE:逆起電力定数[Vs/rad]
ω:回転速度[rad/s]
この関係を実際のモータで計測してみると図2.8 のようなきれいな直線になります。
実は、逆起電力定数KEとトルク定数KTは同じもので、これは、次のようにして証明できます。
コイル巻数をNとすると、発生電圧eと逆起電力定数KEとは、次の関係になります。
e = 2RNBLω = KEω ……(2.8)
ここで、(2.7)式に(2.4)式のKT=2RNBLを代入して、両辺をωで割れば、
KT = KE ……(2.9)
となります。
DCモータにおいてKTとKEが同じということは、どんな意味をもつのでしょうか。
それは、簡単にいえばモータとは、電気-機械間の双方向エネルギー変換器であるという意味なのです。
そして、エネルギー変換を「電気→機械」の方向で見たのがフレミング左手の法則で、その変換係数がKTであると解釈できます。
一方、「機械→電気」の方向で見たのがフレミングの右手の法則で、その変換係数がKEになるというわけです。このように、KTとKEは同じものですが、本書では変換の方向が明らかになるようにするため、今後もKTとKEは使い分けることにします。
モータの発電作用を見る
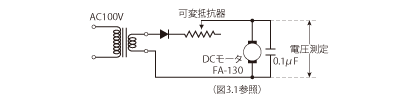
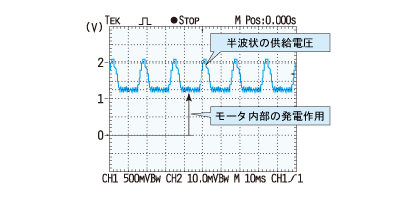
発電作用は、モータに電流が流れて回転しているときにも発生しています。その様子を見るため、図2.9 のように降圧した交流をダイオードで半波整流した電源で、先ほどのモータを回してみましょう。
入力は正弦波の半分のはずなのに、モータ端子間電圧を観察すると図2.10 のような波形が観測されます。これがモータの内部発電作用で発生した(2.7)式の電圧(逆起電力)です。
電圧の釣り合い
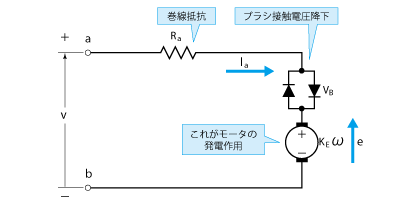
発電作用が、モータ内部でどのような働きをしているかを表したのが、図2.11 です。図では、外部電圧vに対して、巻線抵抗Raによる電圧降下RaIa、ブラシ接触部の電圧降下VBおよび、モータの回転による内部発電電圧(逆起電力)e=KEωの和が釣り合っています。
ここで、外部電圧が高くなるとどうなるでしょう。
- ①巻線抵抗Ra両端の電圧差が大きくなり、回路電流Iaが増える
- ②電流が増えると、トルクが増加する
- ③トルク増加によりモータは加速され、回転が速くなる
- ④回転が速くなると、逆起電力が高くなる
この順序で、新しい安定状態になるまで回転速度が高まります。
つぎに、電圧が一定の状態で、外部負荷が増えたらどうでしょう。
- ①回転速度が低下すると、逆起電力も低下する
- ②その結果、巻線抵抗部に電圧差が生じて電流が増える
- ③電流が増えると、モータのトルクが強くなり外部負荷と釣り合う
今度は、モータが前より低い速度で安定します。
DCモータには、
- ・負荷が同じなら電圧を高くすると速度が上昇する
- ・負荷が増えると回転速度が低下してトルクが増える
という性質があります。つまり、いままで別のものと考えていた左手の法則と右手の法則による作用がモータの中に同時に存在し、この両者が釣り合ってモータの回転速度が決まっていたのです。
回転速度とトルクの関係
DCモータの回転速度とトルクの関係をグラフに表すと図 2.12 のような関係が得られます。
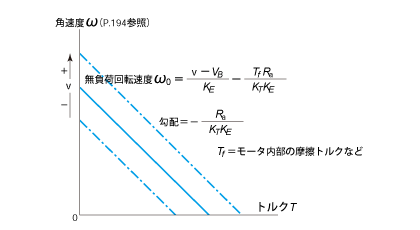
供給電圧が一定の時、DCモータの特性は、このグラフのように右肩下がりの直線になります。
直線の左上端では無負荷時の角速度、右下端では起動時のトルクがわかります。また、供給電圧が高くなると直線は右上に平行移動し、電圧が低くなると左下に平行移動します。
先ほどDCモータには、電流に比例してトルクが増える性質があることを知りました。今度は、電圧を高めると回転速度が上昇する性質があることがわかりました。これは、制御にとって極めて都合の良い性質です。
もう一つ注目したい性質として、DCモータはT=KT(2.3式)の関係から、速度ゼロでも電流に比例したトルクを発生します。このことは、位置決め制御において大きな外力が加わっても、電流を制御して停止位置を保持できることを意味します。
これは、誘導モータやステッピングモータにはない、DCモータとブラシレスDCモータだけが持つ性質です。これらのモータがサーボ制御に用いられるのは、停止位置を保持できる性質があるからです。
<一口コラム> N-T特性
回転速度の単位を[rpm]にして、トルクとの関係を示した特性をN-T特性と呼ぶことがあります。
鉄心(コア)のないモータの実例
これまで説明した、鉄心のないモータにもっとも近い実用モータが、コアレスモータまたはムービングコイルモータと呼ばれるモータです。
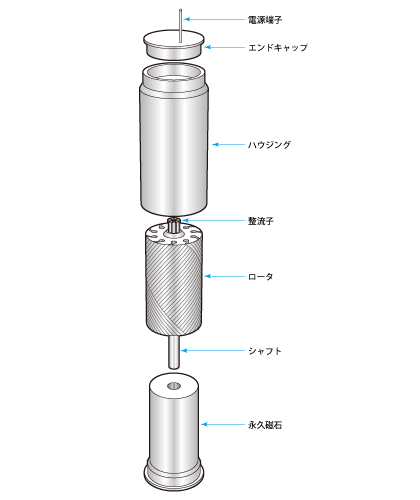
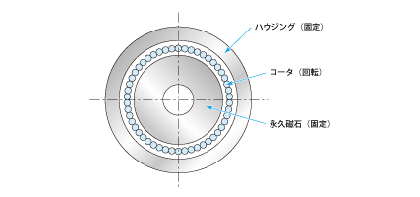
コアレスモータは、名前が示すように、ロータ(回転子)に鉄心を使わず、樹脂で固めたコイルをロータにしたモータです。その例を図2.13 に、断面図を;図2.14 に示します。
コアレスモータには、コイルを平板状にしたタイプもあります。このモータは、プリント基板を作るのと同じ製法で作られたことから、プリントモータと呼ばれています。
ロータに鉄を用いないと、次のような多くの利点がでます。
- ●慣性モーメントが小さく機敏な動作ができる(*注)
- ●ロータに磁石の吸着力が作用しないので回転が滑らか
- ●インダクタンスが低いので整流時に火花が発生しにくい
- ●火花が発生しにくいとブラシ摩耗が少ない
- ●摩耗が少なければ金属ブラシが使え、接触電圧降下が減り、モータ効率が高くなる
欠点もあります。
- ●小型化や高性能化のためには、アルニコ磁石や希土類磁石など高価な磁石が必要
- ●コイルの製造コストが高い
- ●貴金属ブラシや貴金属整流子を用いると製造コストが高くなる
コアレスモータは、大量かつ安価な供給を求められるDCモータの主流になりにくく、小型機器、計測機器あるいは精密制御用のモータに使用されてきました。
しかし、近年は小さなモータという長所を活かして携帯電話の振動モータ(ページャモータ)として使用され、いつの間にか身近なモータのひとつになってきました。
コアレスモータではありませんが、円筒状の鉄心にコイルを巻き付けたモータもあります。このモータは、通常のDCモータと比べ、鉄心に溝がないのでスロットレスモータと呼ばれます。
スロットレスモータはコイルと共に、鉄心も回転しますが、動作原理はコアレスモータとほぼ同じです。スロットレスモータは、ブラシレスDCモータが登場するまで、高性能制御用モータとして用いられました。
- *注:プリントモータはコイルが扁平なため慣性モーメン(moment of inertia)は小さくない

