モータの不思議と更なる可能性の探究
第十一回 非ローレンツ力の不思議
NIDECはモータの総合メーカであると認識されてきました。モータにはさまざまな種類と,直径2mm程の小型から水力発電所の大型まで豊富です。
社内研修のある場面のことを語ります。研究所で仕事をする事務系の社員を対象とした技術関連の研修でした。講師は情熱にあふれる30代前半の若手ですが,研修を受ける側には60代前半の優秀な管理職の方がいました。Mさんとします。
2日間の研修が終えたときMさんは,「なぜモータの種類がこんなに多いか不思議ですね。」とおっしゃったのです。傍から見ていた筆者には,それは講師に対する質問というよりは感嘆のように聞こえました。
久しぶりにモータの不思議について書くのですが,いつか書かなくてはならないと思ったのは,Mさんのこの一言がきっかけです。この問いに対する私の答えは一つでありません。どのような仕事をなさる方かによって答え方が変わります。ここでは,モータの物理学と数学に関心があってモータの設計に携わる人とロボットや自動車にモータを使う技術者を読者の対象として論じてみようと思います。世界中のどんな本にも書かれてはいないことです。
テーマは『非ローレンツ力とは何か?』です。
これについて書こうと思ったもう一つ理由は,学位論文として磁気浮上の研究をした若い研究者からの問いがきっかけでした。モータに関して学術的な取り組みをする若い人にも,ローレンツ力とは何か?それに対して非ローレンツ力とは何か,またこれら2つの力の関係はどんなものなのか知っておくべき知識であることを認識したのです。これは基本問題というよりも,高度な数学と物理的意味の両方を宿していると思います。
まずローレンツとはオランダの物理学者 Hendrik Lorentz(1853-1928)です。彼を有名にしたのはアインシュタインの相対性理論の鍵になるローレンツ変換です。ローレンツ変換とはいったい何のことか?については次回の課題にしようと思います。
電気や磁気を使うモ―タの原理を説明するときに,よく持ち出されるのが図1です。(a)は 2個の電荷の間にはたらく力の関係です。(b)は1820年のエルステッドの実験とされる磁針と電流の作用です。どちらも力の作用ですが,相違点は(a)は直線的な力であるのに対して(b)は直角的な力です。モータの電気力学を論じるときに,ローレンツ力と言えばこの2つをさします。物理学としてはここで基本を語ったことになります。数学の基礎である幾何学では,直線と直角を最初に論じた後,その2つを基盤としてさまざまな定理が構築されます。それに比べると,工学やモータの設計と制御のからの視点は奥深く,幅広いのです。
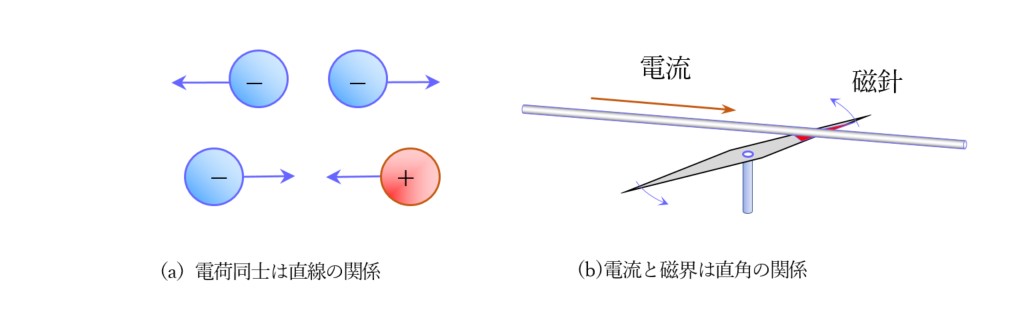
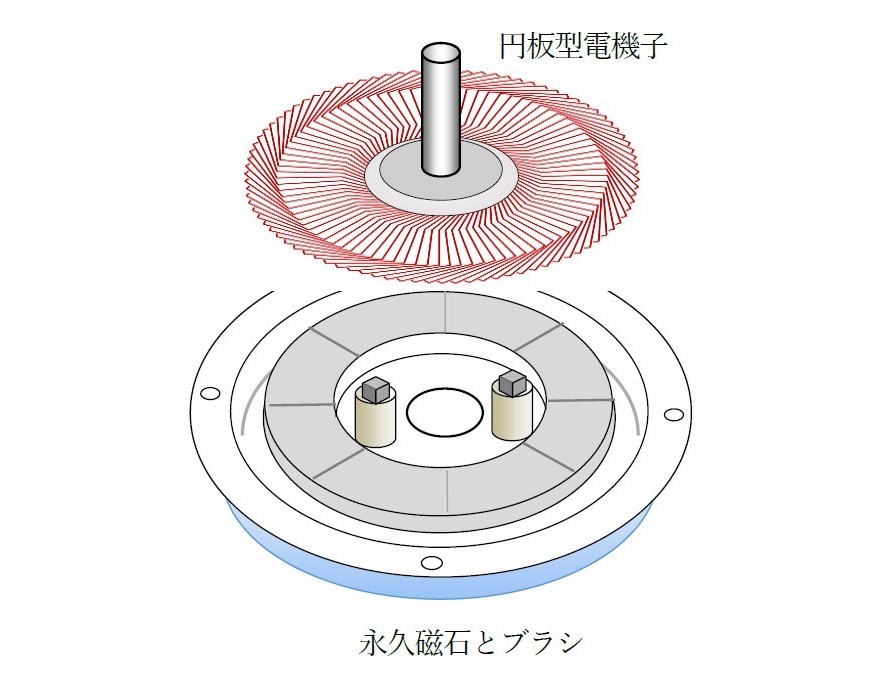
(a)の直線的な原理はモータとしてはほとんど使われていません。では(b)の直角的は原理が多いに使われているでしょうか? 図2のプリントモータと図3に示すコアレスモータです。そして,もう一つが図4のHDD装置の磁気ヘッドの制御に使われるmoving-coil motorです。
これから察知できるように,精密モータ,特殊モータという印象が強く,産業用,鉄道や電気自動車などの大型モータにはローレンツ力は使われないようです。用途がずっと多く経済効果の大きいのがこれから語る非ローレンツ力を使う設計です。


ここまでを総括:
モ―タは電気を使って力を発生して回転運動を作る装置であるが,図1(a)のような単純な直線的なベクトル力を使う用途は希でしかない。それに比べると(b)のように磁界を取り入れて直角的な力を利用する事例はずっと多い。けれども大きな産業になるのは,これを超える原理―非ローレンツ力―である。
******
永久磁石利用のスロット型モータの場合
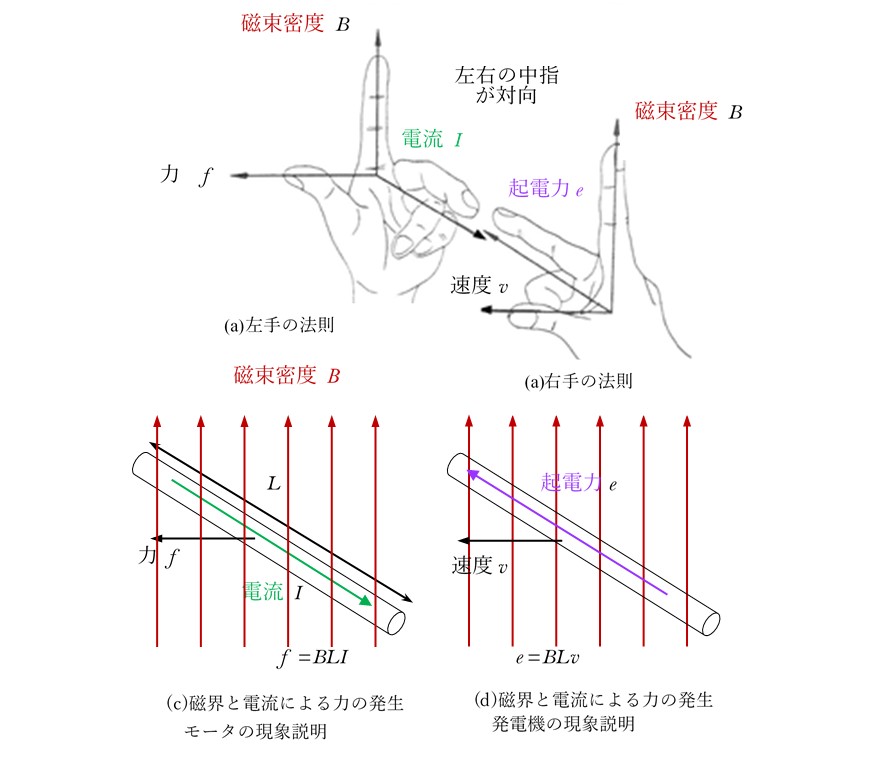
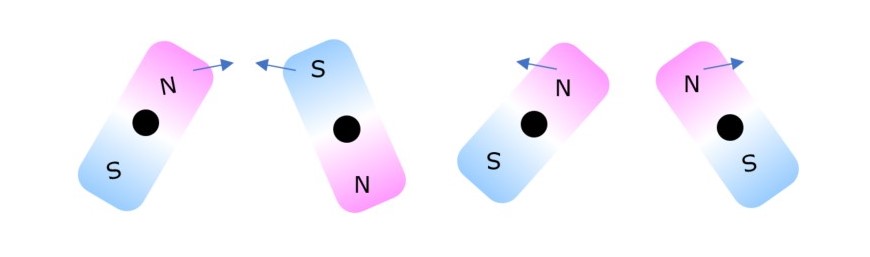
磁気ローレンツ力は図5に示すようにフレミングの左手の法則やBIL則として知られています。これとは異なる原理のトルク(回転力)としては,図6に示すように,永久磁石のN極とS極の間で作用する引力とNとNあるいはSとSの同極間の反発力です。ここには電流が無いのでローレンツ力の作用はないはずです。
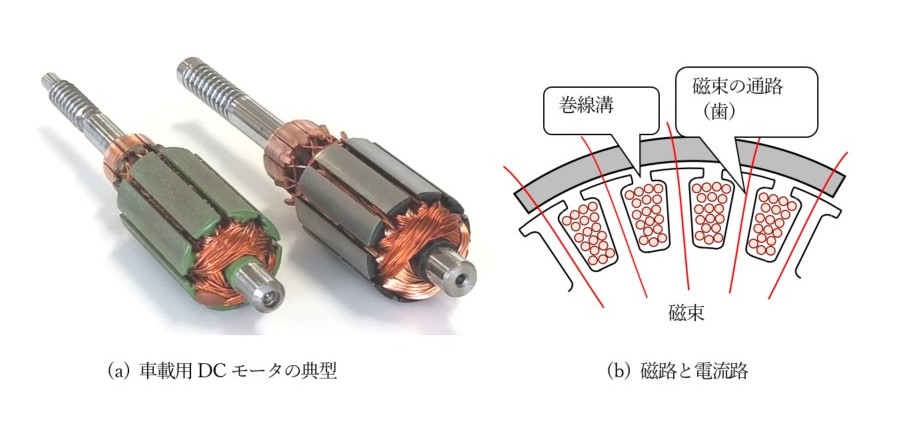
ここでさらに考えます。図7(a)は典型的なDCモータのロータです。自動車電装品として多数使われているものです。図7(b)はこのような構造の場合にローレンツ力が作用するかしないかを考察するための図です。図示と説明から分かるように,ローレンツ力は作用しないはずです。
ヒステリシスの利用 自起動同期モータ
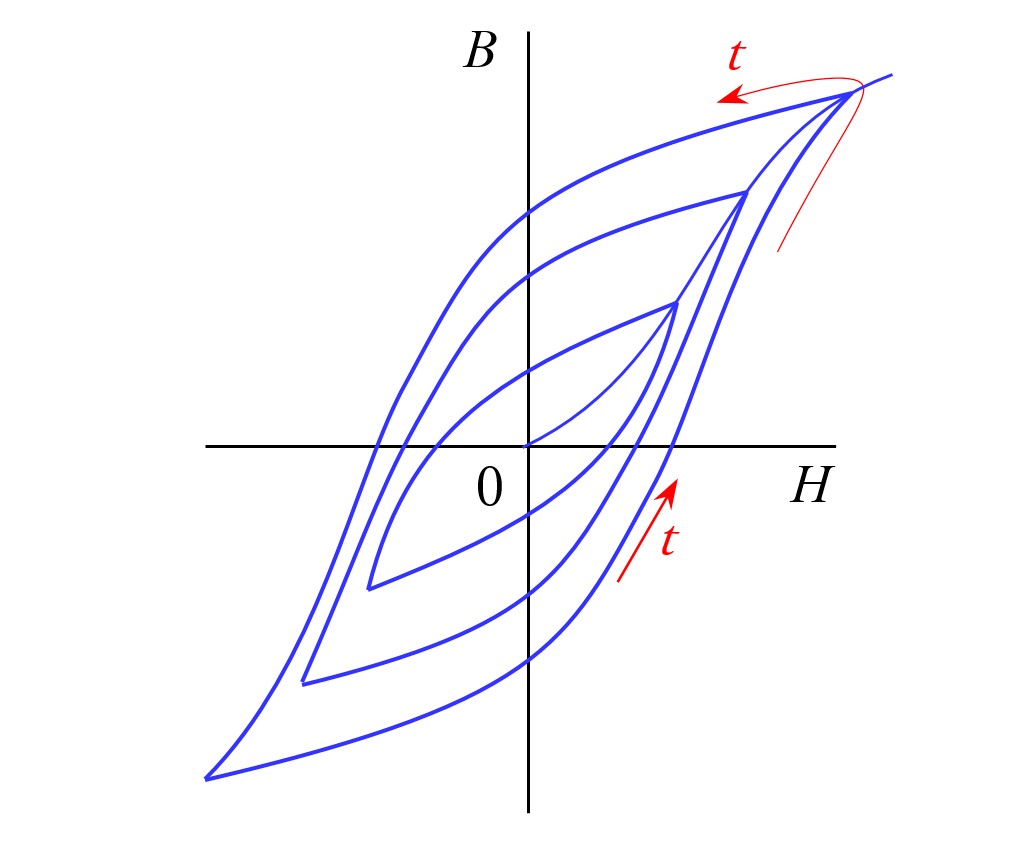
モ―タが発生する力についてさらに考えた人がいます。完全な永久磁石ではなく不完全な永久磁石によるトルクの可能性です。それが図8のヒステリシスと呼ばれる磁気的な現象によるものです。
これを図9で説明します。(a)は均質のリング状の不完全な永久磁石を素材とするヒステリシスモータのロータです。(b)は4個の永久磁石を使うロータであり,今日ではブラシレスモータとして大量に利用されるものです。
ステータは巻線によって磁界を形成して高速回転磁界をつくります。ここに(c)のように,ロータと組み合わせたときに,これら2つのロータの違いが分かります。ヒステリシス磁鋼の(a)はすんなりと回りまって,1秒間の回転数は東京では25ですが富士川以西の京都や大阪では30です。これらの数値は交流の周波数(50あるいは60ヘルツ)の半分です。半分になる理由は使った巻線が4極巻きだからです。(d)は4極磁界の意味を示します。図9のステータには8極巻線も設置されているので,これに給電すると回転速度は東京12.5と大阪15 rounds per secになります。もし2極巻線であればそれぞれ50と60 rounds per sec です。このように電源周波数の整数分の1の速度で回るモータを同期モータと呼びます。4極の永久磁石を貼り付けた(b)のロータの場合には8極巻線ではトルクが発生しません。2極巻線でも回りません。
なめらかに起動して同期速度に自然に達するのは極めて有難い特質です。
(b)の永久磁石ロータの場合には,回らないで振動しています。自起動できないので回るためには仕掛けが必要であり,それを備えるのがブラシレスDCモータです。その仕掛けの説明は割愛します。
ロータは起動できるでしょうか?イナーシャ(慣性モーメント)が大きいと起動できないでガタガタと振動します。(a)は永久磁石として弱い磁鋼です。この場合にはロータにヒステリシス現象が起きて起動して加速して最終的に回転磁界の速度で回ります。

ユーイングからシュタインメッツへ
弱い永久磁石を使うと自起動できる同期モータができることに気づいたのがシュタインメッツであり,1920年ごろと伝えらます。しかしヒステリシス自体に意味を感じてhysteresisを造語したのは日本政府がスコットランドから招聘したJames Ewing(1855-1935)でした。場所は東京神田の工部大学校(東京大学工学部の前身)です。1882年のことです。彼のもとで学んだ“優秀な”日本の科学技術者がなぜこのモータを発明できなかったのでしょうか? これは,覚える・暗記する能力と新しいことを発見する思考力は別物であることを示す好事例と言えそうです。
ティアのトルク式へ
シュタインメッツの原理発見から一歩進めて実用化のための理論を構築したのがティア(B.R.Teare, 1907-不詳)でした。非ローレンツ力の数学表現を,1940年にAIEE(American Institute of Electrical Engineers)という学術誌に読みやすい編集で発表したのです。ただし非ローレンツ力という用語はありません。彼の論文はテープレコーダ用のモータの進展に決定的な影響を与えました。(ティアのことはホームページに書いてあります。)
ティアのトルク式は図10のように記されているのですが,簡潔に書き直すと次式です。
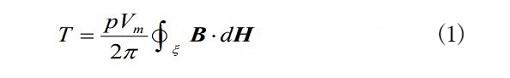
です。ここに現れる積分
![]() がキー(開鍵)です。
がキー(開鍵)です。![]() はロータの磁石材料の体積であり,
はロータの磁石材料の体積であり,![]() はステータ巻線の磁極数です。
はステータ巻線の磁極数です。
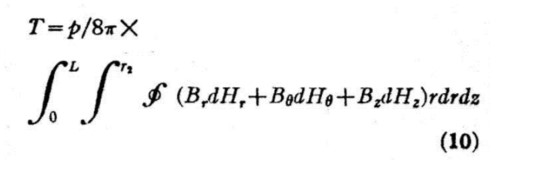
筆者がこの論文をある会社の役員から頂いたのは24歳の時でした。まだ頭が柔らかい青年でしたので,ヒステリシスによる損失の式が![]() あり,媒介変数(時間
あり,媒介変数(時間![]() と空間円周座標
と空間円周座標 ![]() )の違いによって損失と出力が同じ形式で示されることの不思議の背景には相対性理論(時空の一体性)があることを感じました。もちろん,大学での数学,物理学,電磁気学の学習と大学院修士課程での思考の訓練があってのことです。
)の違いによって損失と出力が同じ形式で示されることの不思議の背景には相対性理論(時空の一体性)があることを感じました。もちろん,大学での数学,物理学,電磁気学の学習と大学院修士課程での思考の訓練があってのことです。
それから2年後に,長倉安次郎という数学者に出あって,この積分をスティルチェス積分と呼ぶこと,そして通常のリーマン積分との関係を教授いただきました。すると頭脳に閃いたのです。ティアの式は磁気ヒステリシスに限定されることなく,すべてのモータに適用できるはずだ!
そして英国の物理学者でマクスウェルと共同研究をしたポインティングの理論と,ドイツの数学者ガウスの空間積分定理を使って説明しようと思いました。その結果として導かれたのが次のトルク式です。
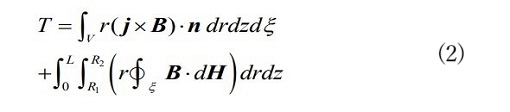
<補足>ガウスの定理:
任意のベクトル![]() に対して次の関係が成り立つ:
に対して次の関係が成り立つ:

これは真空中の面上の積分をロータを含む体積積分に置きかえる定理です。
任意のベクトル![]() として
として![]() (ポインチングのベクトル)とします。そしてマクスウェル方程式を使うと次式が得られます。
(ポインチングのベクトル)とします。そしてマクスウェル方程式を使うと次式が得られます。

さらに微分と積分のテクニックとして
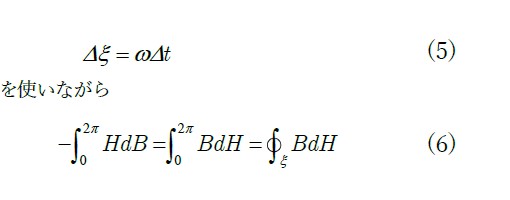
の積分定理に着目し,時間微分![]() から
から
![]() を取り去り
を取り去り
![]() に着目します。
次に体積積分の中の
に着目します。
次に体積積分の中の![]() に着目すると
に着目すると ![]() が出てきます。
が出てきます。
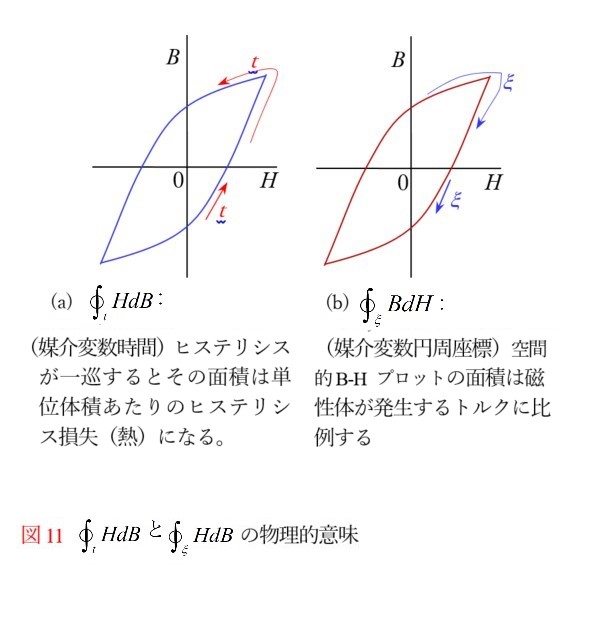
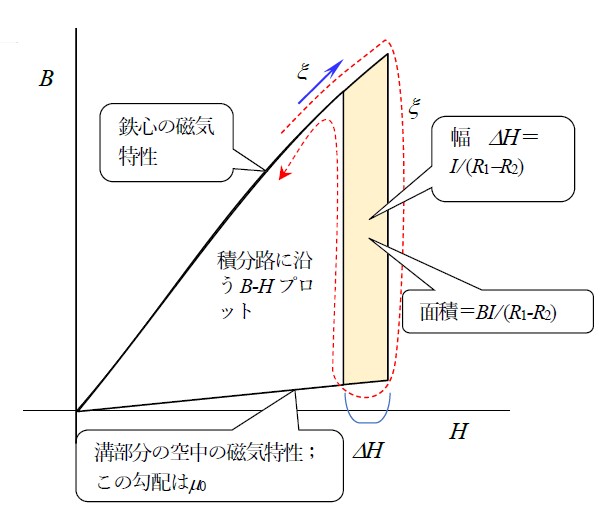
図11(a)に示すように,時間的に一巡する![]() ヒステリシスの面積は鉄損の一種ですが,同図(b)と図9(e)に示しているように,ある瞬間の空間的に1周する
ヒステリシスの面積は鉄損の一種ですが,同図(b)と図9(e)に示しているように,ある瞬間の空間的に1周する![]() プロットの面積は回転力(トルク)であり,それに角速度
プロットの面積は回転力(トルク)であり,それに角速度 ![]() を掛けると動力です。このように,数学的には動力の計算は(
を掛けると動力です。このように,数学的には動力の計算は(![]() )平面の図形の計算―つまり幾何学―になります。図12にはもう一つの数学的な意味を描いています。
)平面の図形の計算―つまり幾何学―になります。図12にはもう一つの数学的な意味を描いています。
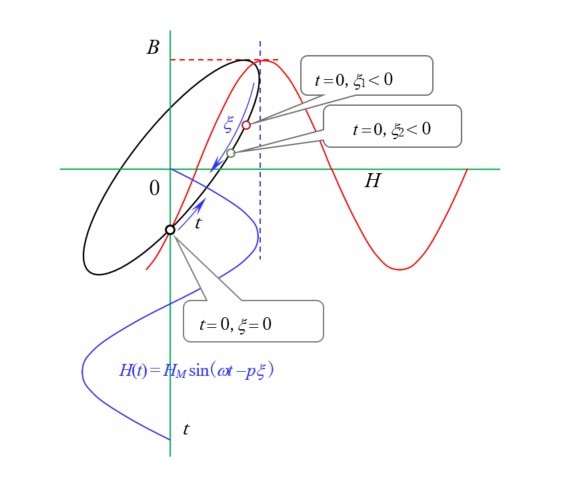
 の変化に対して
の変化に対して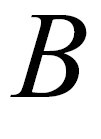 は時間的に遅れている。
は時間的に遅れている。 ここで,これに関係する新しい不思議を語ります。これを誘導モータの理論に当てはめるとどうなるかが第1歩で,第2歩はクローポール型ステッピングモ―タの不思議です。
誘導モータの場合:ローレンツ力との対比
第2項 奥深い電磁的非ローレンツ力の利用
では,非ローレンツ力について考察してみます。経済ベースではおそらく99%のモ―タが非ローレンツ力を使っているのですが,これを工学としてしっかりと論じた専門書に出会っていません。この課題は積分![]() の意味の追究になります。
の意味の追究になります。
(2)式を導くときに大きなヒントになったのが誘導モータの古典的な等価回路論でした。モータ内の磁気回路を見事に交流回路網に対応づける計算手法です。そこには二次入力(secondary input)という概念があります。その概念をポインティングの電磁エネルギー理論で説明しなおしたのです。誘導機のすべり ![]() による扱いに特殊相対性理論を持ち込んでみました。対象とする系に運動物体がないときには
による扱いに特殊相対性理論を持ち込んでみました。対象とする系に運動物体がないときには ![]() で運ばれるエネルギーはすべてジュール熱になります。しかし注意が必要です。アインシュタインの主張
で運ばれるエネルギーはすべてジュール熱になります。しかし注意が必要です。アインシュタインの主張
物理現象はどんな座標系でも同じように記述されるはずだ!
に若干の言い過ぎがありそうです。どんな座標系でもポインティングベクトル ![]() によって物体に流れこむエネルギーは熱に変換されるように記述される,と主張するのであれば,それは疑問に思えます。筆者は,ここでエネルギー保存則を考えなおして,真空をとおる電磁エネルギーは機械エネルギーにも変換されるはずだ!として理論をつくり直してみました。
によって物体に流れこむエネルギーは熱に変換されるように記述される,と主張するのであれば,それは疑問に思えます。筆者は,ここでエネルギー保存則を考えなおして,真空をとおる電磁エネルギーは機械エネルギーにも変換されるはずだ!として理論をつくり直してみました。
誘導モ―タのロータ鉄心は図13のような断面をしています。溝にアルミあるいは銅が充填されていて,ここに電流が流れます。しかし磁界は鉄心を通ります。ですから導体にはローレンツ力による力は作用しません。しかし出力軸にはしっかりとトルクが発生します。つまり,電機子鉄心には力が作用しているはずです。
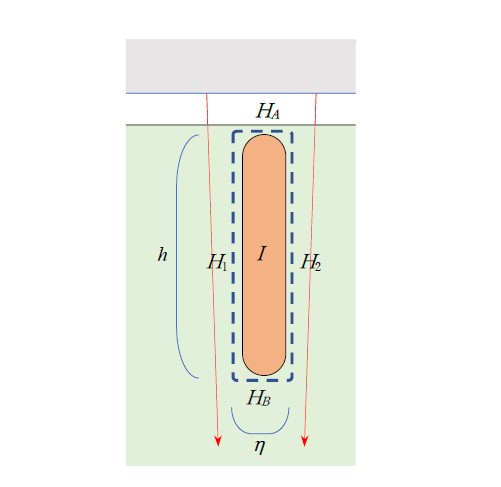
図13には2つの積分路を示しています。水平線は図9(e)に記したトルク計算の積分路の一部であり,もう一つはアンペアの周回積分![]() の一巡路です。これを,図14の(閉溝構造で)描き直します。すると,積分則は次式になります。
の一巡路です。これを,図14の(閉溝構造で)描き直します。すると,積分則は次式になります。
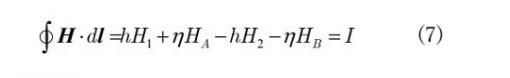
ここで, ![]() と
と ![]() は磁界強度の横向きの成分であり無視できるものとすると,(7)は次のように簡単になります。
は磁界強度の横向きの成分であり無視できるものとすると,(7)は次のように簡単になります。

これより,溝の両側の ![]() の差
の差![]() は電流
は電流 ![]() に比例して
に比例して
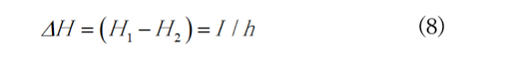
であることが分かります。
次は,図13の水平線で示す![]() の積分路に関係する計算です。1溝にわたる部分の(
の積分路に関係する計算です。1溝にわたる部分の(![]() )トレース図として示すのが図15です。ループが囲む面積はハッチ部分の台形の面積であり,
)トレース図として示すのが図15です。ループが囲む面積はハッチ部分の台形の面積であり,![]() です。ここで
です。ここで![]() から
から![]() までの積分と導体の長さ方向の積分をとると,この導体に作用する非ローレンツ力は
までの積分と導体の長さ方向の積分をとると,この導体に作用する非ローレンツ力は![]() になります。つまりローレンツ力と同じ形になります。本当に導体に磁束が通っていればこの力が導体に作用するのですが,鉄心とスロットの場合には,導体には作用しません。つまり鉄心のどこかに作用するのですが,この数学操作では特定できません。シャフトから得られるトルクとしては検証できると思います。
になります。つまりローレンツ力と同じ形になります。本当に導体に磁束が通っていればこの力が導体に作用するのですが,鉄心とスロットの場合には,導体には作用しません。つまり鉄心のどこかに作用するのですが,この数学操作では特定できません。シャフトから得られるトルクとしては検証できると思います。
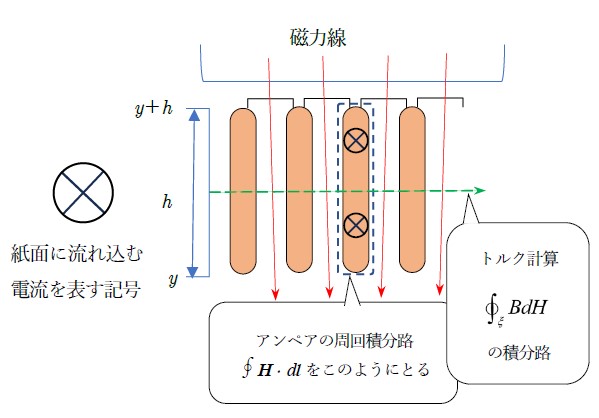
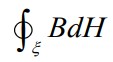 の図形的な計算;1個の溝をまたがる積分
の図形的な計算;1個の溝をまたがる積分ここに現れる不思議の一つは,鉄心の重要性でもあります。磁界を通しやすい鉄心を使わないでローレンツ力を使おうとすると,機械強度的に耐えられるモータがつくりにくいのです。鉄のこの性質は電子のスピンによるものです。このスピンに関心を抱いた一人がアインシュタインでした。1915年の冬にオランダの(Lorentzの娘婿にあたる)ドハース(de Haas)と有名な実験をして,スピンによる磁気モーメントが機械的な運動量に変換されることを確認したのです。しかしスピンというものが分かり始めたのは量子力学が生まれて発展した当時であり,決定的な論文を英国のPaul Dirac (1902-1984)が発表したのは1928年でした。スピンの量子数を天才的な数理の操りで導きだしたのです。
クローポール型PMモ―タではどうなのか
さまざまなモータ構造があるのですが,図16のクローポール型モータは不思議を帯びています。トルク(回転力)の計算は,積分路をクローポール(歯)と関連させてうまく設定することによって,理論的にはできます。もっと踏み込んだときに不思議が現れます。さまざまな構造のモータがあるのですが,クローポール型ステッピングモータの巻線ほど簡単で,しかも無駄のない方式がほかにないのです。IPM(interior permanent magnet)型と呼ばれるEV用トラクションモータが典型ですが,巻線にはコイルエンドという無駄部分があって,これがモータの製造工程で最も厄介な部分の一つです。

それに加えて筆者が思う不思議は,トルクの向きを90°変えるクローポールの機能です。BIL則に対応する左手の法則では電流を運ぶ電線の向きと電磁力は直角の関係にあります。クローポール型のボビン式コイルでは回転の向きを90°変える傘歯車機能が3次元の磁気的構造によって形成されることを示唆します。これこそは非ローレンツ力の不思議です。フレミングの左手と左手の法則を見直して,電気力学の不思議を学び直す価値がありそうです。これは大学では学べない(時空に関する)根本問題と言えます。
結言
非ローレンツ力は鉄の性質と深く関係することを見ました。「鉄」の意味が奥深いです。物理学としては電子のスピンの問題に帰結するのだろうと思います。Mさんの疑問に答えるには,じつは半導体エレクトロニクスとの関係を語る必要があるのですが,それは数冊の本になるかもしれません。モータの技術は,工学としてエレクトロニクスに重ねて台頭しているスピントロニクスの一部門になりそうです。さらに視点を変えると,鉄系金属の産業界へのメッセージになります。企業の事務系,経営戦略系の方々の出番がここにありそうです。
1. B.R. Teare : Theory of hysteresis-motor torque, AIEE, 1940, p.907-12


